7. Yineleme (Tekrarlamalı)

Bilgisayarlar sıklıkla tekrarlayan görevleri otomatikleştirmek için kullanılmaktadır. Aynı veya benzer görevleri hatasız bir şekilde tekrarlama işlemi bilgisayarların iyi yaptığı, insanların ise zorlandığı bir şeydir.

Bir komutlar kümesinin tekrar tekrar yürütülmesi işlemine yenileme (iteration) adı verilir. Yineleme çok yaygın olduğu için, Python bunu kolaylaştırmak için birkaç özellik sağlar. 3’üncü bölümde for deyimini gördük. for deyimi en sik kullanacağınız olacaktır. Fakat bu bölümde biz while deyimine bakacağız. Bu, azıcık farklı durumlarda yenileme yapmanın başka değişik yoludur.

Bu konuya girmeden önce, birkaç fikirin üstünden yeniden geçelim.

7.1. Atama

Daha önce bahsettiğimiz üzere, aynı değişkene birden fazla atama yapılması geçerli bir yöntemdir. Yeni bir atama varolan değişkeninin yeni bir değeri temsil etmesini sağlar ( ve önceki eski değerin temsilliyetini ortadan kaldırır.)

kalan_sure = 15
print(kalan_sure)
kalan_sure = 7
print(kalan_sure)

Bu programın çıktısı:

15
7

Çünkü kalan_sure ilk defa ekrana basıldığında değeri 7’dir, ikinci defada ise 15’dir.

Atama komutu ile bir eşitliği sınayan Boolean ifadesi arasındaki farkı ayırtetmek özellikle önemlidir. Çünkü Python eşit işaretini (=) atama için kullanmaktadır. a = b şeklindeki bir komutu Boolean testi olarak algılamak çekici gelebilir. Matematikte alıştığından farklıdır. Python’da eşitlik ifadesi olarak == kullanıyoruz.

Dikkat ediniz ki eşitlik (==) ifadesi simetrik olmasına rağmen, atama komutu (=) simetrik değildir. Örneğin, a == 7 ve 7 == a deyimleri aynıdır. Fakat Python’da a = 7 ifadesi geçerli olmasına rağmen, 7 = a geçerli bir ifade değildir.

Python’da atama komutu iki değişkeni birbirine eşitler, fakat daha ileriki atamalar bunlardan herhangi birini değiştirebileceğinden, sürekli bu şekilde kalmaları gerekli değildir:

a = 5
b = a # a ve b şimdi eşitler
a = 3 # a ve b artık eşit değiller.

Üçüncü satır a değişkeninin değerini değiştirir ama b değişkeninin değerinin değiştirmez; bu yüzden artık eşit değillerdir (Bazı programlama dillerinde karmaşayı önlemek için <- veya := gibi farklı simgeler atama komutu yerine kullanılmaktadır.) Bazı kişiler değişken isminin seçilmesinin talihsiz olduğu, bunun yerine atanabilir olarak adlandırılması gerektiğini düşünürler. Python dili; C, C++, Java ve C# dillerinde olduğu gibi genel terimbilimini ve işaretleri kullanır. = işaretini atama için, == işaretini ise eşitlik için kullanır.

7.2. Değişkenleri güncellemez

Bir atama komutu yürütüldüğünde, ilk önce sağ taraftakı ifade hesaplanır ( yani atama işaretinden sonra gelen ifade.) Bu bir değer üretir. Sonrasında ise sol taraftaki değişkenin yeni değeri temsil edecek şekilde ataması yapılır.

En yaygın atama biçimlerinden biri güncellemedir. Bir değişkenin değerini eskisine bağlı olarak değiştirmektir. Örnek olarak kalan süreden 40 saniye çıkarmak veya bir skor tabelasına bir eklemek gibi.

n = 5
n = 3 * n + 1

Burdaki 2.satır’ın anlamı: n’nin o andaki değerini al, üç ile çarp, bir ekle ve çıkan sonucu n’e ata. Böylece n artık bu sonuca işaret edecektir. Yukarıdaki iki satırı çalıştırdıktan sonra, n 16 sayısını temsil edecek / işaret edecektir.

Eğer atama yapılmamış bir değişkenin değerini almaya kalkarsanız bir hata oluşur:

>>> w = x + 1
Traceback (most recent call last):
  File "<interactive input>", line 1, in
NameError: name 'x' is not defined

Bu değişkeni güncellemeden önce, onu bir başlangıç değerine ilklendirme (initialize) yapmanız gerekir. Bu ise basit atama komutu ile yapılır:

mac_skoru = 0
...
mac_skoru = mac_skoru + 1

3.satır değişkene 1 ekleyek onu güncellemektedir. Güncellemeler oldukça yaygın olarak kullanılır. Bir değişken üzerine 1 ekleyerek güncelleme işlemine arttırma; değerinden 1 çıkarma işlemine çıkarma adı verilir. Programcılar bazen buna değişkene toslama (bumping variable) olarak da bahsetmektedirler. Bu değişkenini 1 arttırılması ile aynı anlama gelir.

7.3. for döngüsünü tekrar gözden geçirme

for döngüsünün listenin içindeki öğeler üzerinden döngü yaptığını hatırlayınız. Listenin içindeki eleman sırasıyla döngü değişkenine yeniden atanır ve döngünün içindeki gövde çalıştırılır.

for f in ["Jale", "Zerrin", "Burak", "Ahmet", "Zeki", "Tülay",
"Perihan"]:
    davet_et= "Merhaba" + f + ". Lütfen Cumartesi Doğumgünü partime
    gelin."
    print(davet_et)

Liste içindeki bütün öğeleri teker teker taramaya gezinme (traversing) olarak isimlendireceğiz.

Öğeleri sayılardan oluşan bir listenin bütün öğelerini toplayan bir fonksyion yazalım. Bunu ilk önce el ile yapalım ve adım adım nasıl ilerleyeceğimiz fikrini kafamızda oluşturalım. Liste üzerinden bir yere kadar yaptığınız ara toplamı bir kağıt üzerinde, kafanızda veya hesap makinanızda tutmanıza ihtiyaç olacak. Programımızda değişkenlerin olmasının sebebi bir adımdan diğer bir adıma geçerken şeyleri hatırlamaktır. Bu yüzden “ara toplamı” hatırlayacak bazı değişkenlere ihtiyacımız olacak. Bu ara toplamın ilk başlangıçtaki değerini sıfır ile başlatmalıyız (ilklendirmeliyiz.) ve bu listenin öğeleri üzerinden gezinmeliyiz. Ara toplamaya sonraki bir sayıyı eklediğimizde, ara toplamayı güncelleştirmeliyiz.

def toplam(xs):
    """ xs listesi içindeki bütün öğelerin toplar ve bu sonucu geri
    döndürür."""
    ara_toplam = 0
    for x in xs:
        anlik_toplam = anlik_toplam + x
    return ara_toplam

# Aşağıdaki sınamaları, sınama takımına ekleyiniz.
test(toplam([1, 2, 3, 4]) == 10)
test(toplam([1.25, 2.5, 1.75]) == 5.5)
test(toplam([1, -2, 3]) == 2)
test(toplam([ ]) == 0)
test(toplam(range(11)) == 55)  # 11 listeye dahil değildir.

7.4. While deyimi

Aşağıdaki kod parçası while deyiminin kullanışını gösterir:

def kadar_toplam(n):
    """  1 + 2 + 3 + ... n toplamını geri döndürür."""
    ara_toplam = 0
    v = 1 # listenin ilk elemanı
    while v <= n:
        ara_toplam = ara_toplam + v
        v = v + 1 # sonraki öğe
    return ara_toplam # listenin bütün öğeleri toplandı

# Test takımınız
test(kadar_toplam(4) == 10)
test(kadar_toplam(1000) == 500500)

While cümlesini sanki bir ingilizce cümleymiş gibi okuyabilirsiniz. Bunun anlamı: ” v‘nin değeri n‘den küçük ve eşit olduğu sürece, döngü gövdesini çalıştırmaya devam ettir” demektir. Gövdenin içinde (while içindeki girintili kısım v‘nin değerini bir arttırılır. v‘nin değeri n değerini geçince toplam değeri geri döndürülür.

Daha biçimsel olarak, while deyiminin yürütme akışını aşağıda inceleyebilirsiniz:

• 5’inci satırdaki koşulu değerlendir; False veya True değerini üret.
• Eğer değer False ise, while deyiminden çık ve bir sonraki satırdan yürütmeye devam et ( bu durumda 8’inci satır.)
• Eğer değer True ise, while gövdesi içindeki satırları çalıştır (6’ıncı ve 7’inci satır)

Gövde, while deyiminin altında eşit girintiye sahip olan cümleleri içermektedir.

Dikkat ediniz ki, eğer döngü koşulu ilk defa False değerini döndürdüğünde, gövdenin içindeki cümleler asla çalıştırılmaz.

Döngünün gövdesi bir veya birden fazla değişkenin değerini değiştirmelidir ki, koşul (while deyimi) sonunda yanlışlanabilsin ve döngünün bitmesi garanti edilsin. Aksi takdirde döngü sonsuza kadar tekrar edecektir. Bu şekildeki döngülere sonsuz döngü denir. Şampuanların üzerindeki “köpürtün, durulayın, tekrarlayın” işlemi başlı başına bilgisayar bilimcisi için komik kaçabilir çünkü bu döngüyü durduracak bir koşul yoktur.

Burdaki durumda döngünün bir süre sonra sona erdiğini ispatlıyabiliriz. Çünkü n‘nin değerinin sonlu olduğunu biliyoruz ve v‘nin değerinin döngü içinde arttırıldığını görebiliriz. Sonunda v‘nin değeri n‘nin değerini aşacaktır. Diğer başka durumlarda, döngünün sona ereceğini bilmek kolay olmayabilir.

Programcı açısından while döngüsünün onun eşiti for döngüsünden daha fazla emek gerektirdiğini dikkat etmiş olabilirsiniz. while döngüsünü kullanırken, kişi döngü değişkenini kendi yönetmelidir: bu değişkenine başlangıç değeri verin, döngünün sona erip ermediğini sınayın ve döngü gövdesi içindeki değişkeni arttırıldığına emin olun ki döngü sonlanabilsin. Karşılaştırma yapmak için aynı işlemleri for deyimi ile yapan fonksiyonu yazalım:

def kadar_toplam(n):
    """ 1 + 2 + 3 + ... n toplamını geri döndürür."""
    ara_toplam = 0
    for v in range(n+1)
        ara_toplam = ara_toplam + 0
    return ara_toplam

range fonksıyonunun biraz kafa karıştırıcı kullanımını dikkat edin. n‘e bir eklemek zorunda kaldık çünkü range fonksiyonu, içine verdiğiniz değere kadar fakat bu değeri dışarda tutarak bir liste oluşturur. Daha önceki bölümde birim sınama (unit testing) konusuna zaman ayırdığımız için sınama takımı kullanarak yaptığımız hatayı yakalabilirdik.

7.5. Collatz’ın 3n+1 dizisi

Matematikçileri yıllarca yanılgaya düşüren ve kendine hayran bırakan basit bir diziye bakalım. Matematikçiler bu dizi hakkındaki basit soruları bile hala cevaplıyamamaktır.

Bu diziyi yaratmak için kuralımız: Verilen n ile diziye başlayın; eğer n çift ise bunu ikiye bölün, eğer tek ise bu sayıyı 3 ile çarpıp 1 ekleyin. Bu dizi, n 1’e ulaştığında sona erer.

Aşağıdaki Python fonksiyonu bu algoritmayı ifade eder:

def Collatz_dizisi(n):
    """ n'den başlayarak 3n+1 dizisini basar,
    1'e ulaştığında durur.
    """
    while n != 1:
        print(n, end=", ")
        if n % 2 == 0: # n çift sayı
            n = n // 2
        else :  # n tek sayı
            n = 3 * n + 1
    print(n,end=".\n")

Dikkat ederseniz 6’ıncı satırdaki print fonksiyonu fazladan end="," argümanı vardır. Bu bize, print fonksiyonunun ekrana bastığı değişkenden sonra, programcının seçtiği (bu durumda, virgül ve arkasından bir boşluk) karakter dizisini peşisıra basmasını ve alttaki satıra geçmemesini söyler. Böylece döngü içindeki birşey ekrana basıldığında, sayılar arasına virgül gelecek şekilde aynı satıra yazılırlar. Döngü sona erdiğinde 11’inci satırdaki print(n,end=".\n") çağrılacak ve sonrasında ekrana en son n değerini arkasından nokta ve yeni satır gelecek şekilde sonlandıracaktır ( Gelecek bölümde \n‘nin (yeni satır karakteri) ne anlama geldiğini göreceğiz.)

n !=1 döngünün devam etme koşuludur, böylece döngü sonlandırma koşuluna ulaşıncıya kadar çalışmaya devam edecektir ( yani, n == 1.)

Döngü her tekrarladığında, program n‘nin değerinin çıktısını verir ve sonrasında n‘nin tek veya çift olup olmadığını denetler. Eğer çift ise n 2’ye bölünür; eğer tek ise n‘nin değeri n * 3 + 1 ile değiştirilir. Bazı örnekler:

>>> Collatz_dizisi(3)
3, 10, 5, 16, 8, 4, 2, 1.
>>> Collatz_dizisi(19)
19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13,
                    40, 20, 10, 5, 16, 8, 4, 2, 1.
>>> Collatz_dizisi(21)
21, 64, 32, 16, 8, 4, 2, 1.
>>> Collatz_dizisi(16)
16, 8, 4, 2, 1.
>>>

n artabildiği ve azalabildiği için n‘nin 1’e erişip erişemiyeceğine veya programın sonlanıp sonlanmıyacağına dair bir garanti yoktur. n‘nin bazı belirgin değerleri için yürütmenin biteceğini garantiyebiliriz. Örneğin, ikinin kuvvetlerini başlangıç değeri olarak kabul edersek n‘nin her seferinde döngüde ikiyi bölünerek 1’e ulaşılacaktır (her bölünme çift sayı olacaktır.) 16 ile başlayan önceki örneğimiz böyle bir seridir.

Küçük bir sayı ile başlayıp, program sonlanmadan önce yüz adımdan fazla tekrar gerektiren bir dizi bulup bulamıyacağınızı bakın.

Belirgin değerler hariç, Alman matematikçi Collatz tarafından ilginç soru ortaya atılmıştır: Collatz sanısı ( 3n + 1 sanısı olarak da bilinir), n’nin bütün pozitif değerleri için dizi sonlanır. Şimdiye kadar, hiç kimse bunu veya aksini ispatlamış değildir! (Sanı (Conjecture): Bir ifadenin doğru olabileceğini fakat kimsenin emin olamamasıdır.)

“Collatz kuralını kullanarak bütün pozitif sayıların sonunda 1’e yakınsayacağını” sanısının ispatlanması veya aksini ispatlanması için neye ihtiyaç olacağını dikkatlice düşünün. Çok büyük sayıları hızlı bilgisayarlarla sınayabilirsiniz. Şimdiye kadar bütün bu sayılar sonunda 1’de sona eriyor. Fakat kim bilir? Belki de 1’e indirgenimiyen hala test edilmemiş bir sayı vardır.

Eğer 1’e ulaştığıdınızda durmaz, dizinin kendi içinde bir döngüye girdiğine dikkat edeceksiniz: 1, 4, 2, 1, 4, 2, 1, 4 ... Bir olasılık da henüz bizim keşfedemediğimiz hala bazı diziler olmasıdır.

Collatz sanısı hakkında Wikipedia’da bilgilendirici bir makale vardır. Bu dizi başka isimlerlerle de adlandırılır ( Hailstone dizisi, Wonderous sayıları, vb.) Bu makalede kaç tane tam sayının sınandığını ve hepsinin de 1’e yakınsadığını bulacaksınız.

for ve while arasında seçim

Bir döngüye başlamadan önce bir döngü gövdesini kaç kere çalıştıracağınızı biliyorsanız for döngüsünü kullanınız. Örneğin, bir listenin öğeleri üzerinden geziniyorsanız, “listedeki bütün elemanlar” kadar döngü sayısına ihtiyacınız olacağını muhtemelen biliyorsunuzdur. Veya bir tabloyu 12 kere ekrana basmanız gerekiyorsa, kaç kere döngüyü çalıştıracağınızı derhal biliyorsunuzdur.

Örneğin bu hava modellemesini 1000 kere yinele" veya "bir kelime listesi içinden bir kelimeyi ara", "10000'e kadarki bütün asal sayıları bul" gibi işlemler ``for döngüsü için en iyisidir.

İlk duruma biz belirli yineleme olarak isimlendireceğiz: Önceden neye ihtiyaç olucağı konusunda bazı sınırlar olacağını biliyoruz. Belirsiz yineleme ise: Kaç tane yinelem olacağı hakkında emin değiliz; hatta bir üst sınır bile belirleyemiyoruz.

7.6. Programı izlemek

Etkili bilgisayar programları yazabilmek ve programın çalışma modeli hakkında kavramsal bilgi oluşturabilmek için, bir programcının bilgisayar programlarının yürütmesini izleme yeteneğini geliştirmesini gereklidir. İzleme, bir bilgisayar olmayı ve bir örnek programın çalışması sırasında yürütme akışını takip etmeyi gerektirir. Bu takip, herbir komutun çalıştırılmasından sonra bütün değişkenlerin durumunu ve programın ürettiği herhangi bir çıktıyı kaydetmeyi gerektirir.

Bu süreci anlamak için, önceki kısımdaki Collatz_dizisi(3)` çağrımını izleyelim. İzlemenin başında n (parametre) adında 3 ilk değerine sahip bir değişkenimiz vardır. 3, 1’e eşit olmadığından while döngüsü çalıştırılır; 3 ekrana basılır ve 3%2 == 0 deyimi değerlendirilir. Sonuç False olduğundan, else dalı yürütülür ve ve 3 * 3 + 1 işlemi yapılıp sonuç n‘e atanır.

Program akışı süresince olup bittiğini anlayabilmek için şunu yapalım: Bir kağıt üzerinde programın çalıştığı sürece her değişken için bir sütun, çıktılar için ise başka bir sütün yaratalım. İzlememiz aşağıdaki gibi bir şey olacaktır:

n               çıktı
--              ------
3               3,
10

10 !=1 ifadesinin değeri True olduğundan, döngü gövdesi tekrar yürütülecek ve 10 ekrana basılacaktır. 10 % 2 == 0 doğru olduğundan, if dalı yürütülecek ve n 5 olacaktır. İzlemenin sonunda aşağıdaki gibi sonuç olacaktır:

n               output printed so far
--              ---------------------
3               3,
10              3, 10,
5               3, 10, 5,
16              3, 10, 5, 16,
8               3, 10, 5, 16, 8,
4               3, 10, 5, 16, 8, 4,
2               3, 10, 5, 16, 8, 4, 2,
1               3, 10, 5, 16, 8, 4, 2, 1.

İzleme biraz yorucu ve hataya yatkın olabilir (bu yüzden bilgisayarları bu tür işler için kullanıyoruz) fakat bir programcının sahip olması gereken zorunlu yeteneklerden biridir. Bu izlemeden, programızın nasıl çalıştığı hakkında bilgi edinebiliriz. n‘nin kuvveti ikinin katları olur olmaz, programın \(\mathrm{log}_2 n\) sayısı kadar yürütme sonrası döngünün sona ereceğini izleme sayesinde görebilirsiniz. Gövde içindeki çıktı son 1’i basmayacağından, fonksiyonun sonuna özel olarak print fonksiyonunu koyduğumuzu görebilirsiniz.

Programı izleme, kodunuzun tek tek adımlıyarak çalıştırmayla ve bu değişkenleri gözlemlemekle şüphesiz ilgilidir. Bilgisayarı tek tek adımlama için kullanma bizim için daha az hataya sebep olur ve daha uygundur. Programınız karıştıkça kağıt üzerinde izleme zorlaşır. Bilgisayarınızla izleme yapmak çok daha kuvvetlidir ve kodunuza kesme noktası (breaking point) koymak işinizi kolaylıştırır. Kullandığınız programlama arayüzünü (bu kitapta PyScripter) öğrenmek için zaman ayırmanızı şiddetle tavsiye ediyoruz.

Sizin program izleme yapmanızı ve Python kodunun küçük parçalarını anlamanıza yardım edecek oldukça yararlı görselleştirmeli araçlar vardır. Bizim tavsiye edeceğimiz bir tanesini http://netserv.ict.ru.ac.za/python3_viz bağlantısında bulabilirsiniz.

Daha önce chatterbox (geveze, konuşan) fonksiyonlar konusunda uyarmıştık, fakat biz burda onları kullandık. Python’u daha fazla öğrendikçe, üretilen çıktıları bir dizinin içinde nasıl saklayacağımızı göstereceğiz. Böylece fonksiyonları ortasında gereksiz şekilde ortaya çıkıp düşünce yapımızı sekteye uğratan sinir bozucu print fonksiyonlarını kaldırabileceğiz.

7.7. Basamakları sayma

Aşağıdakı fonksiyon bir tam sayının içindeki rakamları (basamakları) sayar:

def rakam_sayisi(n):
    sayac = 0
    while n != 0:
        sayac = sayac+ 1
        n = n // 10
    return sayac

Fonksiyonumuzu, print(rakam_sayisi(710)) çağırdığımızda 3 değerini ekrana basacaktır. Bu fonksiyon çağrımının yürütmesini ( bir kağıt üzerinde veya Pyscripter’in adım adım yürütme özelliğini veya Python visualizer kullanarak) izliyerek çalıştığına dair kendinizi ikna edin.

Bu fonksiyon hesaplamanın sayaç adı verilen önemli bir hesaplama örneğini göstermektedir. sayac değişkeni 0 ile ilklenmekte ve daha sonra döngü gövdesi herbir seferde yürütüldüğünde sayac bir arttırılmaktadır. Döngü tamamlandıktan sonra, sayac‘ın değeri basamak sayısına eşittir.

Eğer sadece 0 veya 5 olan basamakları saymak isteseydik, sayacı arttırmadan önce bir koşul cümlesi koymamız işe yarardı.

def sifir_ve_besleri_say(n):
    sayac = 0
    while n > 0:
    rakam = n % 10
    if rakam == 0 or rakam == 5:
        sayac = sayac + 1
    n = n // 10
    return sayac

sifir_ve_besleri_say(1055030250) ifadesinin 7 döndürdüğünü doğrulayın.

7.8. Kısaltılmış atama

Bir değişkeni arttırma sık karşılaşılan bir şeydir. Python bunun için bır kısaltma sağlar:

>>> sayac  = 0
>>> sayac += 1
>>> sayac
1
>>> sayac += 1
>>> sayac
2

sayac += 1 ifadesi sayac = sayac + 1 yerine geçen bir kısaltmadır. Bu işleci “artı-eşittir” olarak okuyoruz. Arttırma değeri 1 olmak zorunda değildir.

>>> n = 2
>>> n += 5
>>> n
7

Diğer işleçler için de (-=, *=, /=, //= ve %=) kısaltmalar vardır:

>>> n = 2
>>> n *= 5
>>> n
10
>>> n -= 4
>>> n
6
>>> n //= 2
>>> n
3
>>> n %= 2
>>> n
1

7.9. Python’da yardım ve meta-simge (meta-notation)

Python, kendi içinde tanımlanmış fonksiyonları (gömülü fonksiyonları) ve kütüphaneleri için oldukça geniş bir belgeye sahiptir. Bu yardım belgelerine ulaşmanın farklı yolları vardır. PyScripter içinde, Help menü öğesine tıklayın ve Python Manuals‘i seçin. range gömülü fonksiyonu hakkında yardım arayın. Aşağıdaki gibi birşey elde edeceksiniz.

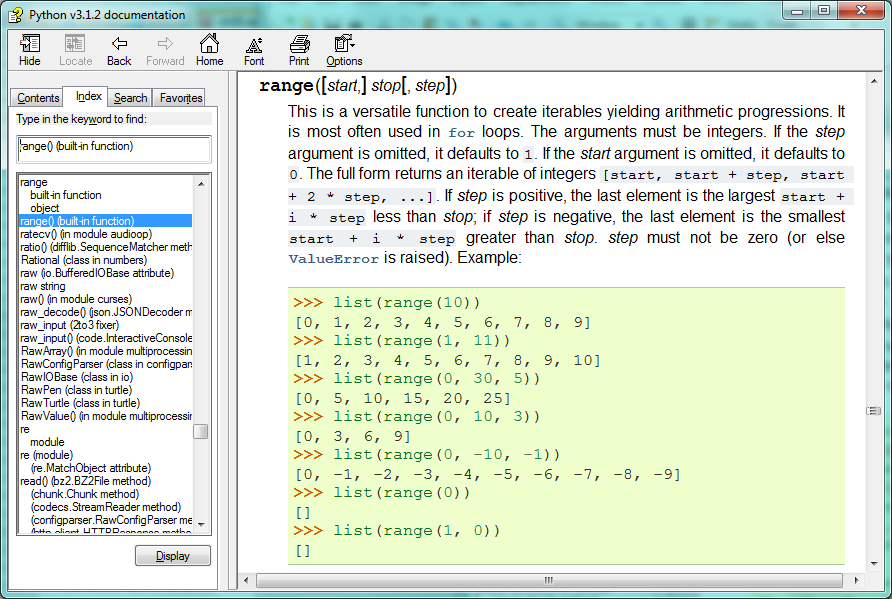
Argümanların bazılarının köşeli parantez içinde olduğuna dikkat edin. Bunlar meta-simge (meta-notation) örnekleridir. Bunlar Python’un söz dizimini tanımlar fakat Python’un içinde yer almazlar. Bu belge içindeki köşeli parantezlerin anlamı, argümanların isteğe bağlı olduğudur; isterse programcı onu ihmal edebilir. Yardım belgesinin ilk satırı bize range fonksiyonunun her zaman bir stop argümanı olması gerektiği, fakat start ve stop argümanlarının seçenekler olduğunu ( aralarında virgül ile ayrılırlar) söyler.

Burdaki yardım belgesi bize range fonksiyonunun 1, 2 veya 3 argümanı olabileceğini gösteriyor. Liste herhangi bir başlangıç değerinden başlayabilir; bu başlangıç değerinden 1’den farklı olarak aşağıya doğru azalabilir veya yukarı doğru artabilir. Bu belge bize argümanların tamsayı olması gerektiğini söylüyor.

Sıkça karşılacağınız siyah ve eğik yazılmış meta-simgeleridir. Siyah yazılmış olanlar bunların anahtar kelime veya simge olduğunu ve nasıl yazılmışsa öyle yazılmalarını; eğik olanların ise ” bir tür” olduğunu belirtir. Böylece aşağıdaki sözdiziminde

for variable in list :

italik kelimeler yerine herhangi bir geçerli değişken (variable) ve listeyi (list) koyabilirsiniz.

print fonksiyonunun (basitleştirilmis) açıklaması bize meta-simgesinin başka bir kullanımını gösteriyor. Üç nokta meta-simgesinin (...) anlamı: Birbirleriyle virgül ile ayrılmış istediğiniz kadar nesne (isterseniz hiç) koyabilirsiniz:

print( [object, ... ] )

Meta-simgesi, söz dizimlerinin şablonunu kesin ve güçlü bir şekilde tanımlamaya olanak verir.

7.10. Tablolar

Döngülerle ilgili güzel şeylerden biri tablo biçiminde veri üretmede yararlı olmasıdır. Bilgisayarlar yokken logaritma, sinüs, cosinüs ve diğer matematiksel fonksıyonların değerlerini insanlar el ile hesaplamak zorundaydı. Bu işi basitleştirmek için matematik kitapları bu fonksiyonların değerlerini veren uzun listeler verirlerdi. Tabloları yaratmak uzun ve sıkıcı işti; üstelik hatalarla doluydu.

Bilgisayarlar sahneye çıktıktan sonra ilk tepkilerden biri, “Müthiş Bilgisayarları tabloları üretmek için kullanabiliriz, böylece herhangi bir hata olmaz.” Bu tepkinin (çoğunlukla) doğru olduğu ortaya ama bu ileriyi göremeyen bir bakıştı. Bilgisayarların ve hesap makinalarının oldukça yaygınlaşmasindan sonra tablolara gerek kalmadı.

Tabi hemen hemen demek gerekiyor. Bazı işlemleri için, yaklaşık bir yanıt üretebilmek ve yaklaşık yanıtı iyileştirmek için hesaplamalar yapmak üzere tabloları kullanıyor. Bazı durumlarda, kaynak olarak kullanılan tablolarda bazı hatalar vardı; bunun en çok bilinen örneği, Intel Pentium tarafından kayan noktalı sayılarda bölme işleminde kullanılan tabloydu.

Her ne kadar bir log tablosu eskisi kadar yararlı olmasa bile, hala yinelemenin güzel bir örneğidir. Aşağıdaki program, sol sütünda değer dizisini ve sağ sütünsa 2 sayısının bu değerden kuvvetinin değerini bir tablo şeklinde verir.

for x in range(13):   # 0'dan 12'ye kadar sayı üret
    print(x, "\t", 2**x)

"\t" ifadesi ** tab karakterini (sekme karakteri)** temsil eder. "t" ifadesindeki "\" kaçış serisi’nin (escape sequence) başlangıcını belirtir. Kaçış dizileri, sekme ve yeni satır gibi görünmez karakterleri temsil eder. "\n" serisi yeni satırı betimler.

Bir kaçış serisi bir karakter dizisinin herhangi bir yerinde bulunabilir; yukarıdaki örnekte tab (sekme) kaçış serisi print fonksiyonu içinde tektir. Bir karakter dizisinin arasına ters bölüyü "\" nasıl yerleştirirsiniz.

Karakter ve karakter dizileri ekranda göründükçe, bir görünmeyen işaretçi olan imleç (cursor), bir sonraki karakterin nereye koyulacağını takip eder. print fonksiyonundan sonra imleç sonraki satırın başına gider.

Tab karakteri imleci bir sekme kadar (Python için 8 boşluk) ileriye götürür. Daha önceki programın çıktısında olduğu gibi, sekmeler metinleri sutünlar şeklinde hizalamak için yararlıdır:

0       1
1       2
2       4
3       8
4       16
5       32
6       64
7       128
8       256
9       512
10      1024
11      2048
12      4096

Sütunlar arasındaki sekmelerden (tab) dolayı, ikinci sütunun konumu birinci sütundaki sayıların basamak sayısına bağlı değildir.

7.11. İki Boyutlu Tablolar

İki boyutlu bir tablo, satır ve sütun kesişimindeki değeri okuduğunuz bir tablodur. Çarpın tablosu buna iyi bir örnektir. 1’den 6’ya kadar çarpım tablosunu yazmak istediğinizi varsayalım.

Başlamak için iyi bir yol, 2’nin katlarını bir satırda basan bir döngü yazmaktır:

for i in range(1, 7):
    print(2 * i, end="\t")
print()

Burda range fonksiyonunu kullandık fakat diziyi 1’den başlattık. Döngü yürütüldükçe i 1’den 6’ya kadar değişir. range‘in oluşturduğu dizinin bütün öğeleri i‘ye atandığında döngü sona erer. Her bir döngü sırasında, 2**i‘nin değerini aralarında bir sekme(t: tab komutu, Python’da 4 boşluk olarak verilir) olacak şekilde görüntüler.

2      4      6      8      10     12

Buraya kadar herşey güzel. Bir sonraki adımımız sarmalama (encapsulate) ve genelleştirme (generalize)dır.

7.12. Sarmalama ve genelleştirme

Sarmalama (encapsulation) bir kod parçasını fonksiyon içerisine koymadır. Böylece fonksiyonlar tarafından sağlanan tüm avantajlardan yararlanmamazı sağlar. Daha önce sarmalama ile örnekler gördünüz; daha önceki bölümdeki bolunebilirmi fonksiyonu gibi.

Genelleştirmeyse, 2’nin çarpım katları gibi özel bir şey alıp onu daha genel bir hale getirmektir. Herhangi bir sayının çarpım katları gibi.

Aşağıdaki fonksiyon bir önceki döngüyü sarmalar ve onu n tamsayısının katlarını basacak şekilde genelleştirir.

def katlari_bas(n):
    for i in range(1,7):
        print(n*i, end="\t")
    print()

Sarmak için yapmamız gereken tek şey fonksiyon ismini ve paratmetre listesini tanımladığımız başlığı ilk satır olarak eklemektir. Genelleştirmek için yapmamız gereken şey, 2’nin değerini n parametresi ile değiştirmektir.

Eğer bu fonksiyonu 2 argümanı ile çağırırsak, daha önce aldığımız çıktının aynısını alırız. Eğer argümanımızı 3 seçersek çıktımız:

3      6      9      12     15     18

Eğer argümanımız 4 olursa çıktımız:

4      8      12     16     20     24

Şimdiye kadar çarpım tablosunu nasıl ekrana basılacağını (katlari_bas fonksıyonunu farklı argümanlarla tekrar tekrar çağırarak) tahmin etmişsinizdir. Aslında başka bir döngü kullanabiliriz:

for i in range(1, 7):
    katlari_bas(i)

Bu yeni döngünün katlari_bas fonksıyonun içindeki döngüye ne kadar benzediğini dikkat edin. Yaptığımız tek şey print fonksiyonunu bir fonksıyan çağrımı katlari_bas koymak oldu.

Bu programın çıktısı bir çarpım tablosudur:

1      2      3      4      5      6
2      4      6      8      10     12
3      6      9      12     15     18
4      8      12     16     20     24
5      10     15     20     25     30
6      12     18     24     30     36

7.13. Daha fazla sarmalama

Sarmalamayı tekrar göstermek için en son kısımdan kodu alalım ve onu bir fonksiyon şekline getirelim:

def carpim_tablosu_bas():
    for i in range(1,7)
        katlari_bas(i)

Bu süreç yaygın karşılaşılan bir geliştirme planıdır. Kodu herhangi bir fonksiyon dışında yazarak veya yorumlayıcıya doğrudan yazarak geliştiririz. Tam olarak çalışan koda ulaştığımızda bu kodu çıkarır ve bir fonksiyon içerisine koyarız.

Bu geliştirme planı eğer programı hangi fonksiyonlara parçalayacağınızı bilmiyorsanız oldukça yararlıdır. Bu yaklaşım siz ilerledikçe programı tasarlamanıza izin verir.

7.14. Yerel Değişken

Aynı değişken i‘yi hem katlari_bas hem de carpim_tablosu_bas fonksiyonlarının ikisinde de nasıl kullanabildiğimizi merak ediyor olabilirsiniz. Bu fonksiyonlardan biri i‘nin değerini değiştirirse bu sorunlara yol açmaz mı?

Yanıt “hayırdır.” Çünkü katlari_bas‘ın içindeki i ile carpim_tablosu_bas‘ın içindeki i aynı değişken değildir.

Bir fonksiyon tanımlanmasının içinde yaratılan değişkenler yereldir; bu değişkenlere tanımlandığı fonksiyonun dışından erişemezsiniz. Bunun anlamı aynı fonksiyon içerisinde tanımlı olmayan, aynı isme sahip birden fazla değişkene sahip olabilirsiniz.

Python bir fonksiyon içindeki bütün cümleleri inceler. Eğer bu cümlelerden biri bir değişkene değer atıyorsa Python bu değişkeni yerel değişken yapar.

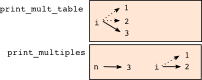
i isimli iki değişkeninin bu program için yiğit diyagramını gösteren şekiller aynı değildir. Bunlar farklı değerleri gösterebilir ve birinin değişmesi diğerini etkilemez.

carpim_tablosu_bas (print_mult_table) içindeki i‘nin değeri 1’den 6’ya kadar gider. Şekilde 3’tür. Bir sonraki döngüde 4 olacaktır. Döngüdeki her seferde, carpim_tablosu_bas fonksiyonu katlari_bas (print_multiples) fonksiyonunun o andaki i değerini argüman olarak çağırmaktadır. Bu değer n parametresine atanmaktadır.

katlari_bas içindeki i değeri 1’den 6’ya kadar değişir. Şekilde 2’dir. Bu değişkeni değiştirmenin carpim_tablosu_bas fonksiyonu içindeki i argümanı üzerinde bir etkisi yoktur.

Aynı isimde farklı yerel değişkenlere sahip olmak sık karşılaşılan bir durumdur ve tamamen geçerlidir. Özellikle i ve j isimleri sıklıkla döngü değişkenleri olarak kullanılmaktadır. Eğer bir başka fonksiyon içerisinde kullandınız diye kullanmamazlık ederseniz, programın okunmasını zorlaştırırsınız.

http://netserv.ict.ru.ac.za/python3_viz/ adresindeki görselleştirici program, iki yerde değişken olarak kullanılan i‘nin nasıl farklı değişkenler olduğunu ve birbirinden bağımsız değerler aldığını göstermektedir.

7.15. break deyimi

break deyimi bir döngünün gövdesini terketmek için kullanılır. Döngü terkedildiğinde gövdeden sonra ilk deyim yürütülür.

for i in [12, 16, 17, 24, 29]:
    if i % 2 == 1:  # Eğer sayı tek ise
       break        #  ... döngüden heme çıkar
    print(i)
print("bitti")

12
16
bitti

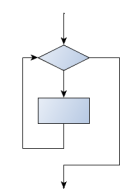
Döngü öncesi sınama: standard döngü davranışı

for ve while döngüleri, gövdenin içindeki deyimleri çalıştırmadan önce başlangıçta sınamalarını yaparlar. Bunlara döngü öncesi sınama denir. Çünkü sınama gövde öncesinde yapılır.

7.16. Döngülerin başka türlü kullanımı

Bazen döngünün yürütülmesi sırasında gövde ortasında sınama yaparak gövdenin sonunda veya başında değil, yürütmenin ortasında gövdeden çıkmak isteriz. Veya gövdenin gövde sonunda sınama yaparak gövdeden çıkış sağlar. Başka diller bunlar için farklı söz dizimi ve anahtar kelimeler kullanabilir, fakat Python while ve if condition: break deyimlerinin birleşimini kullanarak bu işi başarır.

tipik bir örnek olarak program kullanıcısı toplanacak sayıları ekrandan girsin. Kullanıcı daha fazla girilecek sayı olmadığını belirtmek için ekrana özel bir değer girer; bu değer genellikle -1 veya boş bir string olur. Bu tür program ortasında sınama yapmalıdır: Bir sayı girilip, bu sayı sınanıp gövdeden çıkılıp çıkılmıyacağına karar verir.

Ortasında sınama akış diyagramı

toplam = 0
while True:
    cevap = input("Bir sonraki sayıyı girin.  (Sonlandırmak için boş bırakın)")
    if response == "":
        break
    toplam += int(cevap)
print("Girdiğiniz sayıların toplamı", toplam)

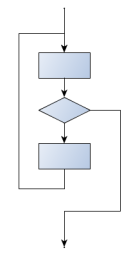
Bu programın gövde ortasında sınama akış diyagramına uyduğuna kendinizi ikna ediniz. 3’üncü satır burda faydalı bir iş yapar, 4. ve 5. satırlar döngüden çıkışı sağlar; eğer bu satırlar çıkış yapmazsa, daha sonraki yenileme başlamadan önce 6’ıncı satır faydalı bir iş yapar.

while bool-tip Boolean ifadesi kullanarak yeniden yenileme yapıp yapmayacağını belirler. while True: deyimi gövde üzerinden sürekli döngü yap demektir. Bu deyimi birçok programcı hemen tanıyacaktır. 2’inci satırdaki ifade döngüyü asla sonlardırmayacaktır, bu yüzden programcı döngü dışına çıkacak (break) bir komut kullanmalıdır. 4. ve 5. satırlar bunu sağlar. Akıllı bir derleyici veya yorumlayıcı 2’inci satırın her zaman doğru olan bir sınama olacağını bildiğinden, her zaman döngünün başına gidip sınama yapmadan döngüyü yürütür. Bu durumda döngümüz her zaman elmas şekline atlama yapacaktır.

Benzer olarak, if koşul: break deyimini gövdenin sonuna taşıyarak gövdein gövde sonunda sınama yaparız. Eğer gövdenin en az bir kere yürütülmesini istiyorsanız gövde sonunda sınama kullanırız (çünkü ilk sınama gövdenin sonunda gerçekleşir). Eğer program bir kişiye karşı en az bir oyun oynamak istiyorsa bu tür kullanım faydalıdır:

while True:
    oyunu_birkere_oyna()
    response = input("Tekrar oynamak istiyor musun?(evet veya hayir)")
    if cevap != "evet":
        break
print("Güle güle!")

İpucu: Çıkış sınamasının nerde yapılacağına karar verin.

Bir şeyi tekrarlamak için bir döngüye ihtiyacınız olduğunu farkettiğinizde, o şeyin sonlandırma sınamasını hakkında düşünün; ne zaman yenilemeyi durdurmayı istiyorsunuz? Sınamayı, ilk yinelemeden önce veya ilk yinelemenin sonunda veya her yinelemenin ortasında sınamayı yapıp yapmak istemediğinize karar verin. Kullanıcı artık daha fazla oyun oynamak istemediğinde, etkileşimli programlar kullanıcıdan bir girdi bekler veya rogramlar yinelemenin sonunda veya ortasında döngüden çıkmak dosyada artık işlenecek veri kalmadığına emin olmalıdır.

7.17. Örnek

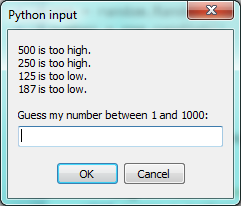
Aşağıdaki program aşağıdaki tahmin etme oyununu uygular:

import random                   # Rastgele sayıları ileriki bölümlerde
rng = random.Random()           # işleyeceğiz.
sayi = rng.randrange(1, 1000) # [1 and 1000) arasında rastgele sayı
                                # üretir.

tahminler = 0
msg = ""

while True:
    tahmin = int(input(msg + "\n 1 ve 1000 arasında bir sayı tahmin et: "))
    tahminler += 1
    if tahmin > sayi:
        msg += str(tahmin) + " çok yüksek.\n"
    elif tahmin < sayi:
        msg += str(tahmin) + " çok düşük.\n"
    else:
        break

input("\n\nMüthiş, {0} tahminde sayıyı buldunuz!\n\n".format(tahminler))

Bu program, matematiğin trichotomy (üçe kısma bölünme) kuralını uygular ( a ve b gerçel sayıları verildiğinde; a > b, a < b veya a == b eşitliklerinden biri mutlaka doğru olmalıdır).

19’uncu satırda input fonksiyonu çağrılır, fakat input fonksiyonundan dönen sonuç ile bir şey yapmayız; bir değişkene bile atamıyoruz. Buna Python’da izin verilir. Burda girdi bekleyen bir pencere ortaya çıkar ve program sonlanmadan önce kullanıcıdan bir cevap bekler. Programcılar, program sonlandığında bu pencerenin açık kalmasını sağlamak (kullanıcın sonucu görmesi için) sıklıkla bu numarayı (kurnazlığı) yaparlar.

Başlangıçta boş bir karakter dizisi olarak; sonradan 7, 13 ve 15 satırlarda msg değişkeninin kullanış biçimine dikkat edin. Döngünün içinden her defasında geçtiğimizde ekranda yazılan mesajı yenileriz. Program bize sonraki tahmini sorduğu yerde bu mesaj bize gerekli yol gösterimini sağlar ( büyük veya küçük sayı girdiğimizi belirtir.)

7.18. Continue (devam) deyimi

Bu bir kontrol akış deyimidir; döngünün o anki adımını bitirir ama döngüye devam eder. Fakat döngü geri kalan yinelemelerine devam eder.

for i in [12, 16, 17, 24, 29, 30]:
    if i % 2 == 1:      # Bu program çift sayıları
       continue         # ekrana basar.
    print(i)
print("bitti")

Bunun çıktısı:

12
16
24
30
bitti

7.19. Daha fazla genelleştirme

Genelleştirmeye başka bir örnek olarak, yalnız sadece altıya altı çarpım tablosu değil; herhangi bir boyutta bir çarpım tablosunu bastırmak istediğimizi varsayalım. carpim_tablosu_bas fonksiyonuna bir parametre eklemeniz gerecekti.

def carpim_tablosu_bas(zirve):
    for i in range(1, zirve+1):
        katlari_bas(i)

7 değerini zirve+1 ile değiştirdik. Eğer carpim_tablosu_bas fonksiyonunu 7 argümanı ile çağırırsak, şu çıktıyı basar:

1      2      3      4      5      6
2      4      6      8      10     12
3      6      9      12     15     18
4      8      12     16     20     24
5      10     15     20     25     30
6      12     18     24     30     36
7      14     21     28     35     42

Bu fena değil; fakat biz muhtemelen aynı satır ve sütuna sahip bir kare tablo istiyoruz. Bunu yapmak için, tablonun kaç sütuna sahip olmasını belirtmek için katlari_bas fonksiyonuna başka bir parametre ekleriz.

Biraz sinir bozucu olmasını sağlamak için, bu parametreye zirve olarak isimlendireceğiz. Bu bize farklı fonksyiyonların aynı isimli parametrelere ( yerel değişkenlerde olduğu gibi) sahip olabileceğini gösterecek. Bütün program aşağıdaki gibidir:

def katlari_bas(n, zirve):
    for i in range(1, zirve+1):
        print(n * i, end="\t")
    print()

def carpim_tablosu_bas(zirve):
    for i in range(1, zirve+1):
        katlari_bas(i, zirve)

Yeni bir parametre eklediğimizde fonksiyonunun ilk satırını (fonksiyon başlığı) değiştirdiğimizi farketmişsinizdir. Buna ek olarak fonksiyonunun çağrıldığı yerleri ( örneğin carpim_tablosu_bas fonksiyonu içinde çağrılan yer) de değiştirmemiz gerekmektedir.

carpim_tablosu_bas(7) fonksiyonunu çağırdığımızda 7x7 boyutlarında tablo üretir:

1      2      3      4      5      6      7
2      4      6      8      10     12     14
3      6      9      12     15     18     21
4      8      12     16     20     24     28
5      10     15     20     25     30     35
6      12     18     24     30     36     42
7      14     21     28     35     42     49

Bir fonksiyonu uygun şekilde genelleştirdiğinizde, planlamadığımız yeteneklere sahip bir program elde ederseniz. Örneğin ab =ba olması dolayısıyla tablodaki her bir girdinin iki kere görüntülendiğini farketmişsinizdir. Mürekkep harcamasını azaltmak için tablonun sadece yarısını görüntülemek istiyebilirsiniz. Bunu yapmak için carpim_tablosi_bas fonksiyonunda bir satır değiştirmeniz gerekir. Aşağıdaki satırı

carpim_tablosu_bas(i,zirve+1)

aşağıdaki şekilde

carpim_tablosu_bas(i,i+1)

değiştirdiğinizde şu sonucu üretirsiniz:

1
2      4
3      6      9
4      8      12     16
5      10     15     20     25
6      12     18     24     30     36
7      14     21     28     35     42     49

7.20. Fonksiyonlar

Şimdiye kadar fonksiyonların faydalarını birkaç kere bahsettik. Bu faydaların tam olarak ne olduklarını merak ediyor olabilirsiniz. Bunlardan bazıları:

1. Büyük bir programı fonksiyonlara parçalamanız ve bu parçalara anlamlı isimler vermek iyi bir akıl yürütme tekniğidir. Gövde sonunda sınama tekniğini gösteren oyunu_birkere_oyna fonksiyonuna bakınız. Bu parçalama, oyununun detaylarını bir kenara koymamamıza izin verdi. Bu bize yalıtılmış program üzerine yoğunlaşmamızı sağlar. Bu fonksiyon, oyuncunun yeniden oyun oynaması hakkındaki seçimini gerçekleştirir.
2. Uzun bir programı fonksiyonlara parçalamanız, programda parçaları birbirinden ayırmanızı sağlayacaktır. Böylece izole bir şekilde hataları ayıklayabilecek, bu farklı parçaların bir bütün olarak davranmasını sağlayabileceksiniz.
3. Fonksiyonlar yinelemenin kullanımını kolaylaştırır.
4. İyi tasarlanmış fonksiyonlar sıklıkla birçok program için yararlıdır. Bir kere fonksiyonu yazdığınızda ve hataların ayıkladığınızda o fonksiyonu tekrar kullanabilirsiniz.

7.21. İkili veri

Python’da simlerden oluşan bir listeyle ve sayılardan oluşan bir listeyi önceden gördük. İleriki konularda bu konuya biraz daha değineceğiz ve verilerinizi temsil etmeninin ileri yöntemlerini göstereceğiz. İkili veri oluşturmak, bunları iki parantez içine koymak kadar kolaydır. Aşağıdaki gibi:

isim_dogumyil = ("Paris Hilton", 1981)

Birçok ikili veri tipini, ikili veri tiplerinden oluşan bir listeye yerleştirebiliriz:

sohretler = [("Brad Pitt", 1963), ("Jack Nicholson", 1937),
                                ("Justin Bieber", 1994)]

Bu gibi yapılandırılmış veri tipleri ile yapabileceğimiz hızlı bir örnek verelim. İlk olarak şöhretleri ekrana basalım:

print(celebs)
print(len(celebs))

[("Brad Pitt", 1963), ("Jack Nicholson", 1937), ("Justin Bieber", 1994)]
3

sohretler listesinin 3 öğesi olduğunu farkedin; herbiri ikili veri tipidir.

1980 yılından önce doğmuş şöhretlerin isimlerini ekrana basalım:

for (nm, yr) in sohretler:
   if yr < 1980:
        print(nm)

Brad Pitt
Jack Nicholson

Bu bize for döngüsü için şimdiye kadar görmediğimiz bir şeyi gösteriyor: tek bir değişken kullanmak yerine (nm,yr) çiftinden oluşan değişken kullandık. Döngü üç kere yürütülür. Her bir yineleme için listedeki çift bir değişkene atanır.

7.22. İçiçe geçmiş veriler için içiçe listeler

Yapılandırılmış veri listesi ile daha fazla haşır neşir olacağız. Aşağıdaki durumda elimizde bir öğrenci listesi var. Her bir öğrencinin ismi, öğrencilerin kayıt oldukları derslerden oluşan başka bir liste eşlenmiştir:

ogrenciler = [
    ("John", ["CompSci", "Physics"]),
    ("Vusi", ["Maths", "CompSci", "Stats"]),
    ("Jess", ["CompSci", "Accounting", "Economics", "Management"]),
    ("Sarah", ["InfSys", "Accounting", "Economics", "CommLaw"]),
    ("Zuki", ["Sociology", "Economics", "Law", "Stats", "Music"])]

students isimli değişkene beş öğeli bir liste atadık. Her bir öğrencinin ismini ve kayıt oldukları dersleri ekrana basalım:

# öğrencinin ismini ve kayıtlı oldukları derslerin sayısını basalım.
for (isim, dersler) in ogrenciler:
    print(isim, ", kayıtlı ders sayisi:", len(dersler))

CompSci dersini kaç öğrencinin aldığını şimdi sorabiliriz. Bunun için bir sayaca ihtiyacımız vardır ve her bir öğrenci aldıkları dersleri sınayan ikinci bir döngüye gereksinim duyarız.

# Kaç öğrencinin  CompSci dersini aldığını sayalım.
sayac = 0
for (isim, dersler) in ogrenciler:
    for s in dersler:                 # içiçe geçmiş döngü
        if s == "CompSci":
           sayac += 1

print("Compsci dersini alana öğrenci sayısı:", sayac)

Compsci dersini alana öğrenci sayısı:  3

Sizi ilgilendiren kendi veri tipinizin listesini oluşturmanız gerekir. Örneğin bir CD listesi için şarkı isimlerinin listesi; veya film listesi için her bir film için o filmde oynayan oyuncuların listesi olabilir. Böylece bu listeye şu soruları sorabilirsiniz: ” Angelina Jolie hangi filmlerde oynamıştır?”

7.23. Bir sayının kare kökünü bulmak için Newton yöntemi

Döngüler sayısal hesaplamalarda sıklıkla kullanılır. Bu gibi hesaplamalarda bir yaklaşık tahminle başlanır ve bu tahmin yinelenerek geliştirilir.

Örnek olarak, hesap makinaları ve bilgisayarlar olmadan önce insanlar bir sayının kare kökünü elle hesaplamaları gerekiyordu. Newton iyi bir yöntem kullanarak (Newton’dan uzun yıllar önce bu yöntemin bilindiğine dair kanıtlar vardır.) n değişkeninin kare kökünün bulmak istediğimizi farzedelim. Herhangi yaklaşık değer ile başlarsak, aşağıdaki formül ile daha iyi bir yaklaşıkla değer (başladığımız yaklaşık değeri iyileştirerek) hesaplayabiliriz:

daha_iyi_yaklasik = (yaklasik + n/yaklasik)/2

Burda n değeri, karekökünü hesaplamak istediğimiz değerdir. Bu hesaplamayı, hesap makinası kullanarak birkaç kere yapınız. Her bir yinelemenin sizin tahminizi cevaba daha yakınlaştırdığını görebiliyor musunuz? Algoritmanın çok hızlı bir şekilde cevaba yakınsaması, bu algoritmanın elle hesaplamadaki büyük avantajını gösterir.

Döngü ve bu formülü kullanarak bir önceki yaklaşık değeri daha geliştererek bir sayının kare kökünün hesaplayan bir fonksiyon yazabiliriz (Gerçekte hesap makinası kare kökü bulmak için bu yöntemi kullanır. Belki biraz farklı formül ve yöntem kullanabilir, fakat tahmini sürekli geliştiren yöntemi uygular).

Bu, sonsuz sayıda yineleme problemine örnektir: Tahminimizi geliştirmek ve istedğimiz sonuca ulaşmak için kaç kere yineleme yapmak istediğimizi baştan belirlemek mümkün değildir. Tek istediğimiz sonuca olabildiğince yaklaşmaktır. Bizim yinelemeyi durdurmak için koşulumuz şu olacaktır: bir önceki tahminiz ile formülü kullanarak elde ettiğmiz iyileştirilmiş yaklaşımız birbirine oldukça yakın olduğunda döngümüz duracaktır.

İdeal olarak program durduğunda eski tahmin ile yeni tahminin birbirine eşit olmasını isteriz. Fakat gerçel sayıların bilgisayar aritmetiğinde birbirine tam olarak eşit olması biraz zor durumdur. Çünkü gerçel sayılar tam doğru olarak bilgisayarlarda temsil edilemez ( neticede, pi veya \(\sqrt{2}\) sonsuz sayıda ondalık basamağa sahiptir çünkü bu sayılar irrasyonel sayılardır). Bir döngüyü durdurmasını sınamak için ” a‘nın b‘ye yeterince yakın” olup olmadığını programa sormak gerekir. Bu durdurma koşulu şu şekilde kodlanabilir:

if abs(a-b) < 0.001:  # Bunu daha küçük yaparak doğruluğu
                      # arttırabilirsin.
      break

a ile b arasındaki farkın mutlak değerini aldığımızı farkedin!

Bu problem döngünün ortasında çıkmaya iyi bir örnektir:

def kare_kok(n):
    yaklasik = n/2.0     # Start with some or other guess at the answer
    while True:
        daha_iyi_yaklasik= (approx + n/approx)/2.0
        if abs(yaklasik - daha_iyi_yaklasik) < 0.001:
            return daha_iyi_yaklasik
        yaklasik = daha_iyi_yaklasik

# Test cases
print(kare_kok(25.0))
print(kare_kok(49.0))
print(kare_kok(81.0))

Çıktı şöyle olur:

5.000000000016778
7.0
9.000000000004924

Durdurma koşulunu değiştirerek yakınlaştırmayı geliştirip geliştiremiyeceğine bakınız. Algoritma üzerinden adımlayarak ( hesap makinası kullanarak ) bu doğruluk derecesinin elde edilmesi için kaç yineleme gerektiğine bakınız.

7.24. Algoritmalar

Newton yöntemi bir algoritma örneğidir: Belli bir kategorideki (bu durumda kare kökleri hesaplama kategorisi) problemleri çözmeye yönelik mekanik bir süreçtir.

Bazi bilgilerimiz algoritmik değildir. Örneğin tarihteki olayların zamanlarını öğrenmek veya çarpım tablosunu ezberlemek gibi.

Fakat eldeli toplama, borçlu çıkarma veya uzun bölme işlemleri için öğrendiniz tekniklerin hepsi algoritmadır. Veya tutkulu bir Sudoku bilmecesi çözücüsü iseniz, bu bulmacaları çözmek için belli adımları izliyor olabilirsiniz.

Algoritmanın temel özelliklerinden birisi de, yürütebilmesi için bir akıla ihtiyaç olmamasıdır. Basit kurallara göre her bir adımın birbirini izlemesidir. Algoritmalar yanlız özel bir problemi çözmek için değil genel bir sınıftaki problemleri çözmek için tasarlanmıştır.

İnsanlığa büyük faydaları olan atılımlardan biri, zor problemlerin adım adım algoritmik süreç ile çözülebileceğini ( ve bualgoritmaları uygulamak için yeterli teknolojiye sahip olmak) anlamak olmuştur. Bir algoritmanın yürütülmesi sıkıcı olabilir ve bir akıl, algoritmik veya hasaplamalı düşünce gerektirmeyebilir. Yani algoritma kullanmak ve otomatikleştirmek bir probleme yaklaşmanın temelini oluşturur. Bu algoritmaların yürütülmesi toplumumuzu hızla değiştirmektedir. Bazıları, algoritmik düşünceye ve sürece doğru olan kaymanın toplum üzerindeki etkisinin ilk matbaanın keşfinden daha önemli olacağını ileri sürmektedir. Bir algoritmanın tasarımı, ilginç, zihni zorlayan ve programlamın merkezinde olan bir süreçtir.

İnsanların zorlanmadan veya bilinç dışı olarak doğallıkla yaptığı bazı şeyleri algoritmik olarak ifade etmek zordur. Konuştuğumuz dili anlamak buna güzel bir örnektir. Hepimiz konuşabiliyoruz, fakat hiç kimse nasıl yaptığımızı şimdiye kadar tam olarak açıklıyamamaktadır. En azından bu işlemi bir algoritmik biçimde yapmıyoruz.

7.25. Sözlük

algoritma

Bir sınıf problemi adım adım çözme sürecidir.

gövde

Bir döngü içindeki deyimler

breakpoint (kesme noktası)

Programın yürütülmesinin duracağı (veya kesileceği), böylece programın değişkenlerinin o andaki durumunu incelebileceğiniz veya her bir deyim üzerinden adım adım giderek bunları bir seferde bir yürütme yapabileceğiniz programdaki yer.

bump

Programcı jargonu. Arttırma ile eş anlamlıdır.

continue deyimi

Döngünün o anda kalan kısmının atlanmasını sağlayan deyimdir. Akış döngünün başına gider, koşulu değerlendirir ve uygun şekilde döngüye devam eder.

sayaç

Bir şeyi saymak için kullanılan değişkendir. Genelde başlangıçta sıfıra ilklendirilir (atanırlar) ve döngünün gövdesi içinde arttırılırlar.

imleç

Bir sonraki karakterin nereye yazılacağını tutan görünmez işaretçi.

azaltma

1 çıkarma

kesin yineleme

Gövdenin yürütülme sayısını daha önceden bilme. Bu tür yineleme genellikle for loop kullanılarak gerçekleştirilir.

geliştirme planı

Bir programı geliştirme süreci. Bu bölümde basit, belli şeyleri yaptıran; daha sonra bunları sarıp, genelleştirmesine dayanan bir kod geliştirme süreci anlatılmıştır.

kaçış dizisi

Kaçış karakteri işaretirinin ,\, sağına bir veya daha fazla karakter koyarak bu işaretlerin bazı özel davranışlar sergilemesini sağlar. Örnek olarak \n yeni bir satıra geçmenizi sağlar.

genelleştirme

Gereksiz özel bir ifadeyi (sabit bir değer gibi), uygun bir şekilde genel olan bir ifadeyle (bir değişken veya parametre gibi) değiştirme işlemidir. Genelleştirme kodu çok yönlü yapar, tekrar kullanabilirliğini arttırır, hatta yazılması işlemini kolaylaştırır.

arttırma (arttırmak)

Hem isim ve hem de fiil olarak, arttırma bir değere 1 ekleme anlamına gelir.

sonsuz döngü

Döngüyü sonlandırma koşulunun asla gerçekleşmediği döngü çeşididir.

belirsiz yineleme

Bir döngünün, bir koşul sağlanana kadar devam etmesidir. Örneğin while deyimi bu durum için kullanılır.

ilkleme (değişken)

Bir değişkeni ilklemek (initialize), bir değişkene bir başlangıç değeri verilmesidir. Python’da değişkenlere atama yapılmadıkları sürece varolmadıkları için yaratıldıkları zaman ilklenirler. Bu durum diğer programlama dillerinde geçerli değildir. Bu dillerde ilkleme yapılmadan da değişkenler yaratılabilirler. Bu durumda ya çöp değere (anlamsız değer ) veya program tarafından öntanımlı bir değer (genellikle sıfır) atanır.

yineleme

Program deyimler kümesinin tekrar tekrar çalıştırılması.

döngü

Bitiş koşulu karşılanana kadar tekrar tekrar çalıştırılan bir deyim veya deyimler grubu.

döngü değişkeni

Bir döngü sonlandırma koşulunun parçası olarak kullanılan değişken

meta-simgeleri (meta notation)

Başka simgeleri tanımlamada yardımcı olan ek semböller veya simgeler. Kare parentez, üç nokta ve siyah (harf) meta-simgelerini daha önce değinmiştik. Bunlar Python sözdiziminde seçimlik, tekrarlanabilen, yerine başka bir şey yerleştirmede bize yardımcı olan meta-simgelerdir.

döngü ortası sınama

Gövdenin bir parçasını çalıştıran, daha sonra çıkış koşulunu sınayan; ve bu koşula göre ya döngüden çıkan ya da kalan gövdeyi çalıştan deyimdir. Python’da bunun için özel bir yapı yoktur fakat while ve break deyimlerini birlikte kullanabiliriz.

içiçe döngü

Bir döngü gövdesi içinde bulunan başka bir döngü.

yeni satır

İmleci bir sonraki satırın başına taşıyan özel bir karakter (\n)

döngü sonrası sınama

Bir döngünün bir gövdeyi çalıştırdıktan sonra çıkış koşulunu sınamasıdır. Bu yapı için Python’da özel bir komut yoktur, fakat while ve break deyimlerini birlikte kullanabiliriz.

döngü öncesi sınama

Bir döngünün önceden bir gövdeyi çalıştırıp çalıştırmayacağına sınamasıdır. for and while deyimlerinin her ikisi de döngü öncesi sınama deyimleridir.

tek adımlama (single step)

Programınızı bir anda bir tek adım atarak çalıştırmanızı ve bu adımlama sonucu programınızda meydana gelen değişikleri inceleminizi sağlayan python yorumlayıcı özelliği. Hata ayıklamanıza ve programda neler olduğunu anlamınıza yardımca olur.

tab (sekme)

İmleci bulunduğu satırdan diğer o satırdaki bir tab durma noktasına hareket ettiren özel karakter.

trichotomy (üç parçaya ayırma)

Verilen iki gerçel sayı a ve b arasında burda verilen bağıntılardan birinin mutlaka geçerli olmasıdır: a < b, a > b veya a == b. Eğer iki bağıntının yanlış olduğunu tespit edebilirseniz, geri kalanın doğru olduğunu farzedebilirsiniz.

izleme

Bir programın yürütme akışını elle takip etme; değişken durumlarındaki değişimleri ve üretilen çıktıları kaydetme işlemidir.

7.26. Alıştırmalar

Bu bölüm, bir listenin öğelerinin nasıl toplanacağını ve bu öğeleri nasıl sayacağımızı gösterdi. Sayma örneğimizde ayrıca if deyimi bize yalnızca bazı öğeleri saymamıza yardım etti. Daha önceki bölümde 2harfli_ilk_kelimeyi_bul fonksiyonunun içinde bir koşul gerçeklendiğinde, return deyimini kullanarak bize “erken çıkış” olanağı verdiğini göstermiştik. Şimdi ise break deyimini döngüden çıkmak için ( fonksiyondan çıkmak için break kullanılmaz ve continue ise döngüyü sonlandırmadan o andaki döngüden çıkmak için kullanılır).

Listeleri oluşturma, toplama, sayma , sınama koşulları ve erken çıkış işlemleri zengin yapı taşlarıdır. Bunları çeşitli yollarla birleştirerek birbirinden farklı birçok fonksiyon yaratabilirsiniz.

Yukarıdaki yapi taşlarını kullanarak ilk altı soru için fonksiyonları yazabilmelisiniz.

1. Bir liste içinde kaç tane teksayı olduğunu sayan bir fonksiyon yazınız (İpucu: Bu fonksiyon bir listeyi parametre olarak alsın. Mesela listemiz xs = [1,2,3,5,8,20,23] olsun.)

1. Bir liste içindeki çift sayıları toplasın.

1. Bir liste içindeki negatif sayıları toplasın. (xs = [-1, -3, 5,2,-7])

1. Bir listenin içinde verilen kelimeler arasından 5 harflilerin sayısını bulsun (xs = [“ahmet”, “ozhan”, “şener”, “naz”, “gül”]

1. Bir liste içindeki sayıları ilk çift sayıya rastlayan kadar toplayan (çift sayı dahil değil) bir fonksiyon yazınız. (xs = [ 1, 11, 13, 14, 15,12])

1. Kelimelerden oluşan bir listede, “sam” kelimesine kadarki (sam kelimesi de dahil) kaç kelime olduğunu sayan bir fonksiyon yazın. ( Bunun için bir sınama testi yazın. “sam” kelimesi listede yoksa ne oluyor?)

2. Newton yönteminde tanımlanan kare_kok fonksiyonunda daha_iyi_yaklasik her hasaplandığında ekranda görüntüyelen bir print fonksiyonu ekleyin. Fonksiyonuun değiştirdiğiniz halini 25 argümanı ile çağırıp sonuçları kaydedin.

3. carpim_tablosu_bas fonksiyonun son sürümünün yürütülmesini izleyin ve nasıl çalıştığını anlamaya çalışın.

4. n’inci sayıya kadar üçgensel sayılar basan (triangular numbers) ucgensel_sayi_bas(n) bir fonksiyon yazınız. Bu fonksiyonu ucgensel_sayi_bas(5) aşağıdaki çıktıyı üretmeli:

   1       1
   2       3
   3       6
   4       10
   5       15
   

   (ipucu: üçgensel sayının ne olduğunu internetden araştırın.) .. sourcecode:: ignore

   def ucgensel_sayi_bas(n): i = 1 while i <=n:

   print (i,”t”);print (i*(i+1)/2) i +=1

5. asal_sayimi isimli bir fonksiyon yazınız. Bu fonksiyon, tek bir argüman alsı; eğer argüman asal sayı ise True, değil ise False döndürsün. Fonksiyonunu aşağıdaki durumlar için sınayın:

   test(asal_sayimi(11))
   test(not asal_sayimi(35))
   test(asal_sayimi(19911121))
   

   Son durum doğum gününüzü sınamalıdır. Asal sayı olan bir günde mi doğdunuz? 100 kişilik bir sınıfta, kaç kişinin asal sayı doğum gününe sahip olduğunu düşünüyorsunuz.

6. Bölüm 3’de